Vor einiger Zeit wurde ich durch einen Beitrag auf Instagram inspiriert, eine 3-dimensionale geometrische Figur (hier: Tetraeder bzw. Ikosaeder) mit LEDs zu bestücken, um daraus eine Art Kunstobjekt zu machen. Die Idee war, einen kleinen Mikrocontroller (Arduino bzw. ATtiny) zu verwenden, um LEDs vom Typ WS2812B anzusteuern, um somit das volle Farbspektrum auszuschöpfen.
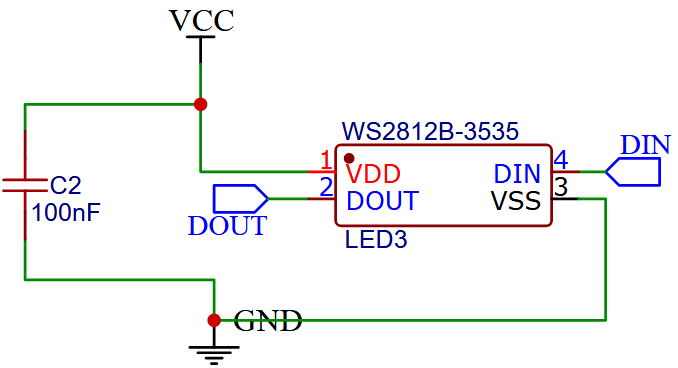
Um solch einen 3-dimensionalen Körper zu erstellen, habe ich mich dazu entschieden, ein Modul zu erstellen, welches jeweils eine Fläche des Objektes darstellen soll. Auf jeder dieser identischen Platinen (PCB) sitzt jeweils eine WS2812B-LED. Der Aufbau dieses Platinen-Moduls ist recht einfach, da die WS2812B außer einem Stützkondensator keine weiteren Komponenten verlangt.

Da ich mich für geometrische Objekte mit gleichseitigen Dreiecken als Flächen entschieden hatte, musste die Platine ein entsprechendes Layout besitzen. Leider besitzt EasyEDA kein exaktes Werkzeug, um eine Platine in anderen Winkeln als 90° zu layouten, daher ist der folgende Aufbau nur näherungsweise möglich gewesen.
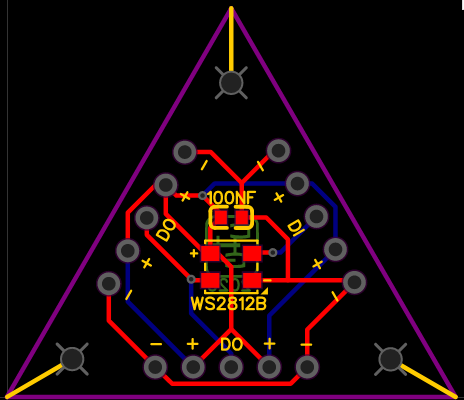
Das obige Layout übergab ich an JLCPCB, einem in China ansässigen Platinenhersteller, der mir nach recht kurzer Zeit 50 gefertige Platinen zugeschickt hat.
Der grundlegende Aufbau eines WS2812B-Moduls wurde ja schon in einem vorherigen Beitrag beschrieben, allerdings sind bei der hier verwendeten SMD-3535-Packung die Anschlüsse nicht beschriftet. Für die meisten Fälle sollten die folgenen Anschlüsse festgelegt sein:
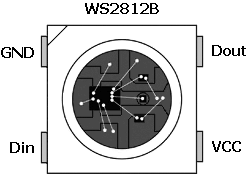



Um zunächst die Funktionalität eines Moduls nach dessen Fertigung zu testen, habe ich folgende Schritt getan.







Der folgende Sketch soll den bzw. die WS2812B-Module testen. Dabei wird im Sekundentakt jeweils eine der
drei Hauptfarben aufleuchten. Wenn später mehrere Modul zusammengeschaltet getestet werden sollen, dann
muss die Konstante LED_AMOUNT nur auf die entsprechende Anzahl an Platinen (=LED-Modulen)
gesetzt werden. (Es wird hier die Library Adafruit_NeoPixel
verwendet)
#define PIN_LED 9
#define LED_AMOUNT 1
#include <Adafruit_NeoPixel.h>
Adafruit_NeoPixel led = Adafruit_NeoPixel(LED_AMOUNT, PIN_LED, NEO_GRB + NEO_KHZ800);
void setup()
{
led.begin();
}
void loop()
{
showAllColor(led.Color(50, 0, 0));
delay(1000);
showAllColor(led.Color( 0, 50, 0));
delay(1000);
showAllColor(led.Color( 0, 0, 50));
delay(1000);
}
void showAllColor(uint32_t color)
{
for(byte i=0; i<LED_AMOUNT; i++) {
led.setPixelColor(0, color);
}
led.show();
}
Die geometrische Figur des Tetraeders besteht
definitionsgemäß aus vier dreieckigen Seitenflächen, und daher müssen vier der oben genannten Polyeder-Modul mit
den Komponenten verlötet werden.
Der exakte Winkel zwischen jeweils benachbarten Flächen beträgt: 70° 31' 44".
Dies errechnet sich aus arccos(1/3)

DI zu DO.




Der folgende Sketch zeigt eine kleine Leucht-Demonstration, wobei zunächst helle Lichtblitze zufällig auf den Flächen des Tetraeders entstehen und nach kurzer Zeit ein regenbogenartiger Farbwechsel. Der Teil des Codes mit dem Farbübergang wurde von rainbow-pixels abgleitet.
#define LED_PIN 9
#define LED_AMOUNT 4
#include <Adafruit_NeoPixel.h>
Adafruit_NeoPixel led = Adafruit_NeoPixel(LED_AMOUNT, LED_PIN, NEO_GRB + NEO_KHZ800);
void setup()
{
led.begin();
randomSeed(analogRead(0));
resetLeds();
}
void loop()
{
strobeLeds(led.Color(0, 50, 50));
rainbowLeds(50);
}
void resetLeds()
{
for (byte i = 0; i < LED_AMOUNT; i++) {
led.setPixelColor(i, led.Color(0, 0, 0));
}
led.show();
}
void rainbowLeds(byte cycleDelay)
{
byte rgb[3] = {255, 0, 0};
for (byte dC = 0; dC < 3; dC++ ) {
byte iC = dC == 2 ? 0 : dC + 1;
for (byte i = 0; i < 255; i++ ) {
rgb[dC]--;
rgb[iC]++;
for (byte a = 0; a < LED_AMOUNT; a++ ) {
led.setPixelColor(a, rgb[0], rgb[1], rgb[2]);
}
led.show();
delay(cycleDelay);
}
}
}
void strobeLeds(uint32_t color)
{
for (byte iter = 0; iter < 200; iter++) {
for (byte i = 0; i < LED_AMOUNT; i++) {
led.setPixelColor(i, led.Color(0, 0, 0));
if (random(0, 33) == 0) {
showColor(i, color, 25);
showColor(i, led.Color(0, 0, 0), 1);
}
delay(5);
}
}
}
void showColor(byte ledIndex, uint32_t color, byte showDelay)
{
led.setPixelColor(ledIndex, color);
led.show();
delay(showDelay);
}
Ein größerer geometrischer Körper, der aus 20 gleichseitigen, dreieckigen Seitenflächen besteht, ist der
Ikosaeder. Hier müssen also 20 der oben
genannten Polyeder-Modul mit den Komponenten verlötet werden.
Der exakte Winkel zwischen jeweils benachbarten Flächen eines Ikosaeders beträgt: 138° 11' 23".
Dies errechnet sich aus arccos(-sqrt(5)/3)
