"Zelluläre oder auch zellulare Automaten dienen der Modellierung räumlich diskreter dynamischer Systeme, wobei die Entwicklung einzelner Zellen zum Zeitpunkt t+1 primär von den Zellzuständen in einer vorgegebenen Nachbarschaft und vom eigenen Zustand zum Zeitpunkt t abhängt." (Quelle: Wikipedia)

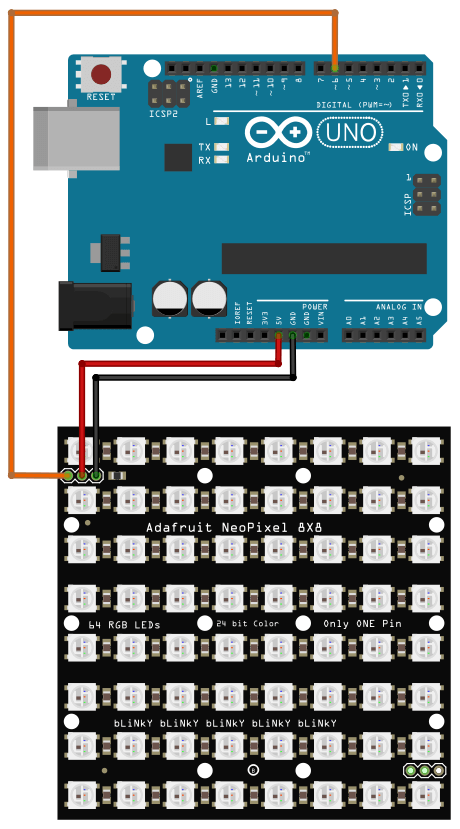
Die folgenden Experimente beschäftigen sich mit zellulären Automaten, die auf eine 8x8-Matrix von RGB-LEDs dargestellt werden. Gesteuert wird dies über einen Arduino-Mikrocontroller.
"Conways Game of Life ist ein vom Mathematiker John Horton Conway 1970 entworfenes Spiel, basierend auf einem zweidimensionalen zellulären Automaten." (Quelle: Wikipedia)
#include <Adafruit_NeoPixel.h>
#define PIN_LED_MATRIX 6
#define FIELD_WIDTH 8
#define FIELD_HEIGHT 8
#define DELAY 150
Adafruit_NeoPixel pixels = Adafruit_NeoPixel(FIELD_WIDTH*FIELD_HEIGHT, PIN_LED_MATRIX, NEO_GRB + NEO_KHZ800);
byte ledMapping[FIELD_WIDTH*FIELD_HEIGHT] = {
0, 1, 2, 3, 4, 5, 6, 7,
8, 9, 10, 11, 12, 13, 14, 15,
16, 17, 18, 19, 20, 21, 22, 23,
24, 25, 26, 27, 28, 29, 30, 31,
32, 33, 34, 35, 36, 37, 38, 39,
40, 41, 42, 43, 44, 45, 46, 47,
48, 49, 50, 51, 52, 53, 54, 55,
56, 57, 58, 59, 60, 61, 62, 63
};
byte field[FIELD_WIDTH][FIELD_HEIGHT];
byte fieldLast[FIELD_WIDTH][FIELD_HEIGHT];
void setup()
{
pixels.begin();
randomizeField();
}
void loop()
{
showLeds();
saveFieldState();
generateNextGeneration();
delay(DELAY);
}
void randomizeField()
{
byte rnd = 0;
randomSeed(analogRead(0));
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
field[y][x] = random(2);
}
}
}
void saveFieldState()
{
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
fieldLast[y][x] = field[y][x];
}
}
}
void generateNextGeneration()
{
byte neighborSum = 0;
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
neighborSum = getNeightborSum(x, y);
if (fieldLast[y][x] == 0) {
if (neighborSum == 3) {
// populate if 3 neighours around it
field[y][x] = 1;
}
} else {
if (neighborSum < 2 || neighborSum > 3) {
// die if only one neighbour or 4 or more neighours
field[y][x] = 0;
}
}
}
}
}
byte getNeightborSum(byte x, byte y)
{
byte sum = 0;
for(int j = -1; j<=1; j++) {
for(int i = -1; i<=1; i++) {
if (j==0 && i==0) {
continue;
}
if (x+i<0 || x+i>FIELD_WIDTH-1) {
continue;
}
if (y+j<0 || y+j>FIELD_HEIGHT-1) {
continue;
}
sum += fieldLast[y+j][x+i];
}
}
return sum;
}
void showLeds()
{
byte i = 0;
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
if (field[y][x] == 1) {
pixels.setPixelColor(ledMapping[i], pixels.Color(0, 10, 0));
} else {
pixels.setPixelColor(ledMapping[i], pixels.Color(0, 0, 0));
}
i++;
}
}
pixels.show();
}Diese Demo ist direkt abgeleitet von "Conway's Game of Life", wobei die Zellen nicht direkt sterben können, sondern erst eine gewisse Zeit altern.
#include <Adafruit_NeoPixel.h>
#define PIN_LED_MATRIX 6
#define FIELD_WIDTH 8
#define FIELD_HEIGHT 8
#define DELAY 50
#define MAX_BRIGHTNESS 10
#define FADE_STEP 1
Adafruit_NeoPixel pixels = Adafruit_NeoPixel(FIELD_WIDTH*FIELD_HEIGHT, PIN_LED_MATRIX, NEO_GRB + NEO_KHZ800);
byte ledMapping[FIELD_WIDTH*FIELD_HEIGHT] = {
0, 1, 2, 3, 4, 5, 6, 7,
8, 9, 10, 11, 12, 13, 14, 15,
16, 17, 18, 19, 20, 21, 22, 23,
24, 25, 26, 27, 28, 29, 30, 31,
32, 33, 34, 35, 36, 37, 38, 39,
40, 41, 42, 43, 44, 45, 46, 47,
48, 49, 50, 51, 52, 53, 54, 55,
56, 57, 58, 59, 60, 61, 62, 63
};
byte field[FIELD_WIDTH][FIELD_HEIGHT];
byte fieldLast[FIELD_WIDTH][FIELD_HEIGHT];
void setup()
{
pixels.begin();
randomizeField();
}
void loop()
{
showLeds();
saveFieldState();
generateNextGeneration();
delay(DELAY);
}
void randomizeField()
{
byte rnd = 0;
randomSeed(analogRead(0));
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
field[y][x] = random(MAX_BRIGHTNESS/2) * 2;
}
}
}
void saveFieldState()
{
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
fieldLast[y][x] = field[y][x];
}
}
}
void generateNextGeneration()
{
byte neighborSum = 0;
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
neighborSum = getNeightborSum(x, y);
if (fieldLast[y][x] == 0) {
if (neighborSum == 3) {
field[y][x] = MAX_BRIGHTNESS; // newborn cell
}
} else {
field[y][x] -= FADE_STEP; // cell gets older
}
}
}
}
byte getNeightborSum(byte x, byte y)
{
byte sum = 0;
for(int j = -1; j<=1; j++) {
for(int i = -1; i<=1; i++) {
if (j==0 && i==0) {
continue;
}
if (x+i<0 || x+i>FIELD_WIDTH-1) {
continue;
}
if (y+j<0 || y+j>FIELD_HEIGHT-1) {
continue;
}
if (fieldLast[y+j][x+i] > 0) {
sum++;
}
}
}
return sum;
}
void showLeds()
{
byte i = 0;
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
if (field[y][x] > 0) {
pixels.setPixelColor(ledMapping[i], pixels.Color(0, field[y][x]/2, field[y][x]));
} else {
pixels.setPixelColor(ledMapping[i], pixels.Color(0, 0, 0));
}
i++;
}
}
pixels.show();
}"Die Ameise ist eine Turingmaschine mit einem zweidimensionalen Speicher und wurde 1986 von Christopher Langton entwickelt. Sie ist ein Beispiel dafür, dass ein deterministisches (das heißt nicht zufallsbedingtes) System aus einfachen Regeln sowohl für den Menschen visuell überraschend ungeordnet erscheinende als auch regelmäßig erscheinende Zustände annehmen kann." (Quelle: Wikipedia)
#include <Adafruit_NeoPixel.h>
#define PIN_LED_MATRIX 6
#define FIELD_WIDTH 8
#define FIELD_HEIGHT 8
#define ANT_AMOUNT 1
#define DELAY 150
Adafruit_NeoPixel pixels = Adafruit_NeoPixel(FIELD_WIDTH*FIELD_HEIGHT, PIN_LED_MATRIX, NEO_GRB + NEO_KHZ800);
byte ants[ANT_AMOUNT][3];
byte field[FIELD_WIDTH][FIELD_HEIGHT][2];
byte ledMapping[FIELD_WIDTH*FIELD_HEIGHT] = {
0, 1, 2, 3, 4, 5, 6, 7,
8, 9, 10, 11, 12, 13, 14, 15,
16, 17, 18, 19, 20, 21, 22, 23,
24, 25, 26, 27, 28, 29, 30, 31,
32, 33, 34, 35, 36, 37, 38, 39,
40, 41, 42, 43, 44, 45, 46, 47,
48, 49, 50, 51, 52, 53, 54, 55,
56, 57, 58, 59, 60, 61, 62, 63
};
void setup()
{
pixels.begin();
randomSeed(analogRead(0));
spawnAnts();
}
void loop()
{
showLeds();
iterateAnts();
delay(DELAY);
}
void spawnAnts()
{
for(byte i=0; i < ANT_AMOUNT; i++) {
// Pick a random point and direction to start each ant
// TODO: make sure ants are evenly distributed/can't spawn on top of each other
ants[i][0] = random(0, FIELD_WIDTH);
ants[i][1] = random(0, FIELD_HEIGHT);
ants[i][2] = random(1, 5);
}
}
void iterateAnts()
{
for(byte i=0; i < ANT_AMOUNT; i++) {
bool on = field[ants[i][0]][ants[i][1]][0];
// Flip the state of the led (on/off)
field[ants[i][0]][ants[i][1]][1] = !on;
// If the LED was on, turn the ant 90 degrees right
if(on) {
ants[i][2] = (ants[i][2]%4) + 1;
} else {
// If the LED was off, turn the ant 90 degrees left
ants[i][2] = ((ants[i][2]+2)%4)+1;
}
// Move the ant forward one unit
switch(ants[i][2]){
case 1:
ants[i][1]=(ants[i][1]+1)%FIELD_HEIGHT;
break;
case 2:
ants[i][0]=(ants[i][0]+1)%FIELD_WIDTH;
break;
case 3:
ants[i][1]=(ants[i][1]+FIELD_HEIGHT-1)%FIELD_HEIGHT;
break;
case 4:
ants[i][0]=(ants[i][0]+FIELD_WIDTH-1)%FIELD_WIDTH;
break;
default:
// Should never happen!
ants[i][1]=(ants[i][1]+1)%FIELD_HEIGHT;
break;
}
}
}
void showLeds()
{
byte i = 0;
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
field[y][x][0] = field[y][x][1];
if (field[y][x][1] == true) {
pixels.setPixelColor(ledMapping[i], pixels.Color(0, 8, 10));
} else {
pixels.setPixelColor(ledMapping[i], pixels.Color(0, 0, 0));
}
i++;
}
}
pixels.show();
}Dieser zelluläre Automat simuliert einen Wald inklusive nachwachsender Bäume. Eine genaue Beschreibung der Regeln findet man unter Spreading of Fire
#include <Adafruit_NeoPixel.h>
#define PIN_LED_MATRIX 6
#define FIELD_WIDTH 8
#define FIELD_HEIGHT 8
#define CELL_EMPTY 0
#define CELL_TREE 1
#define CELL_FIRE 2
#define TREE_GROW_TRESHOLD 1 // amount
#define TREE_GROW_CHANCE 1 // in percent
#define TREE_GROW_CHANCE_BONUS 15 // in percent
#define TREE_FIRE_CHANCE 1 // in percent
#define TREE_FIRE_CHANCE_BONUS 70 // in percent
#define FIRE_FADE_CHANCE 95 // in percent
#define DELAY 250
Adafruit_NeoPixel pixels = Adafruit_NeoPixel(FIELD_WIDTH*FIELD_HEIGHT, PIN_LED_MATRIX, NEO_GRB + NEO_KHZ800);
byte ledMapping[FIELD_WIDTH * FIELD_HEIGHT] = {
0, 1, 2, 3, 4, 5, 6, 7,
8, 9, 10, 11, 12, 13, 14, 15,
16, 17, 18, 19, 20, 21, 22, 23,
24, 25, 26, 27, 28, 29, 30, 31,
32, 33, 34, 35, 36, 37, 38, 39,
40, 41, 42, 43, 44, 45, 46, 47,
48, 49, 50, 51, 52, 53, 54, 55,
56, 57, 58, 59, 60, 61, 62, 63
};
byte field[FIELD_WIDTH][FIELD_HEIGHT];
byte fieldLast[FIELD_WIDTH][FIELD_HEIGHT];
void setup()
{
pixels.begin();
initWorld();
}
void loop()
{
showLeds();
saveFieldState();
iterateWorld();
delay(DELAY);
}
void initWorld()
{
randomSeed(analogRead(0));
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
field[y][x] = CELL_EMPTY;
}
}
}
void saveFieldState()
{
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
fieldLast[y][x] = field[y][x];
}
}
}
void iterateWorld()
{
byte treeNeighbors = 0, fireNeighbors = 0;
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
switch(fieldLast[y][x])
{
case CELL_EMPTY:
treeNeighbors = getNeightborSum(x, y, CELL_TREE);
if (treeNeighbors >= TREE_GROW_TRESHOLD) {
if (random(100) < TREE_GROW_CHANCE_BONUS) {
field[y][x] = CELL_TREE;
}
} else {
if (random(100) < TREE_GROW_CHANCE) {
field[y][x] = CELL_TREE;
}
}
break;
case CELL_FIRE:
if (random(100) < FIRE_FADE_CHANCE) {
field[y][x] = CELL_EMPTY;
}
break;
case CELL_TREE:
fireNeighbors = getNeightborSum(x, y, CELL_FIRE);
if (fireNeighbors > 0) {
if (random(100) < TREE_FIRE_CHANCE_BONUS) {
field[y][x] = CELL_FIRE;
}
} else {
if (random(100) < TREE_FIRE_CHANCE) {
field[y][x] = CELL_FIRE;
}
}
break;
}
}
}
}
byte getNeightborSum(byte x, byte y, byte number)
{
byte sum = 0;
for(int j = -1; j<=1; j++) {
for(int i = -1; i<=1; i++) {
if (j==0 && i==0) {
continue;
}
if (x+i<0 || x+i>FIELD_WIDTH-1) {
continue;
}
if (y+j<0 || y+j>FIELD_HEIGHT-1) {
continue;
}
if (fieldLast[y+j][x+i] == number) {
sum++;
}
}
}
return sum;
}
void showLeds()
{
byte i = 0;
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
switch(field[y][x]) {
case CELL_TREE:
pixels.setPixelColor(ledMapping[i], pixels.Color(0, 7, 0));
break;
case CELL_FIRE:
pixels.setPixelColor(ledMapping[i], pixels.Color(7, 0, 0));
break;
default:
pixels.setPixelColor(ledMapping[i], pixels.Color(0, 0, 0));
break;
}
i++;
}
}
pixels.show();
}Hier sind die Regeln des "3a. Waldbrand" noch um einige Zustände und Bedingungen erweitert worden.
#include <Adafruit_NeoPixel.h>
#define PIN_LED_MATRIX 6
#define FIELD_WIDTH 8
#define FIELD_HEIGHT 8
#define CELL_EMPTY 0
#define CELL_TREE_YOUNG 1
#define CELL_TREE_AGED 2
#define CELL_TREE_DRY 3
#define CELL_FIRE 4
#define CELL_GLOWING 5
#define TREE_GROW_TRESHOLD 1 // amount
#define TREE_GROW_CHANCE 1 // in percent
#define TREE_GROW_CHANCE_BONUS 15 // in percent
#define TREE_DRY_CHANCE 15 // in percent
#define TREE_FIRE_CHANCE 1 // in percent
#define TREE_FIRE_CHANCE_BONUS 70 // in percent
#define GLOW_FADE_CHANCE 50 // in percent
#define FIRE_FADE_CHANCE 75 // in percent
#define DELAY 250
Adafruit_NeoPixel pixels = Adafruit_NeoPixel(FIELD_WIDTH*FIELD_HEIGHT, PIN_LED_MATRIX, NEO_GRB + NEO_KHZ800);
byte ledMapping[FIELD_WIDTH * FIELD_HEIGHT] = {
0, 1, 2, 3, 4, 5, 6, 7,
8, 9, 10, 11, 12, 13, 14, 15,
16, 17, 18, 19, 20, 21, 22, 23,
24, 25, 26, 27, 28, 29, 30, 31,
32, 33, 34, 35, 36, 37, 38, 39,
40, 41, 42, 43, 44, 45, 46, 47,
48, 49, 50, 51, 52, 53, 54, 55,
56, 57, 58, 59, 60, 61, 62, 63
};
byte field[FIELD_WIDTH][FIELD_HEIGHT];
byte fieldLast[FIELD_WIDTH][FIELD_HEIGHT];
void setup()
{
pixels.begin();
initWorld();
}
void loop()
{
showLeds();
saveFieldState();
iterateWorld();
delay(DELAY);
}
void initWorld()
{
randomSeed(analogRead(0));
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
field[y][x] = CELL_EMPTY;
}
}
}
void saveFieldState()
{
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
fieldLast[y][x] = field[y][x];
}
}
}
void iterateWorld()
{
byte treeNeighbors = 0, fireNeighbors = 0;
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
switch(fieldLast[y][x])
{
case CELL_EMPTY:
treeNeighbors = getNeightborSum(x, y, CELL_TREE_AGED);
if (treeNeighbors >= TREE_GROW_TRESHOLD) {
if (random(100) < TREE_GROW_CHANCE_BONUS) {
field[y][x] = CELL_TREE_YOUNG;
}
} else {
if (random(100) < TREE_GROW_CHANCE) {
field[y][x] = CELL_TREE_YOUNG;
}
}
break;
case CELL_TREE_YOUNG:
field[y][x] = CELL_TREE_AGED;
break;
case CELL_TREE_AGED:
if (random(100) < TREE_DRY_CHANCE) {
field[y][x] = CELL_TREE_DRY;
}
break;
case CELL_TREE_DRY:
fireNeighbors = getNeightborSum(x, y, CELL_FIRE);
if (fireNeighbors > 0) {
if (random(100) < TREE_FIRE_CHANCE_BONUS) {
field[y][x] = CELL_FIRE;
}
} else {
if (random(100) < TREE_FIRE_CHANCE) {
field[y][x] = CELL_FIRE;
}
}
break;
case CELL_FIRE:
if (random(100) < FIRE_FADE_CHANCE) {
field[y][x] = CELL_GLOWING;
}
break;
case CELL_GLOWING:
if (random(100) < GLOW_FADE_CHANCE) {
field[y][x] = CELL_EMPTY;
}
break;
}
}
}
}
byte getNeightborSum(byte x, byte y, byte number)
{
byte sum = 0;
for(int j = -1; j<=1; j++) {
for(int i = -1; i<=1; i++) {
if (j==0 && i==0) {
continue;
}
if (x+i<0 || x+i>FIELD_WIDTH-1) {
continue;
}
if (y+j<0 || y+j>FIELD_HEIGHT-1) {
continue;
}
if (fieldLast[y+j][x+i] == number) {
sum++;
}
}
}
return sum;
}
void showLeds()
{
byte i = 0;
for(byte y=0; y<FIELD_HEIGHT; y++) {
for(byte x=0; x<FIELD_WIDTH; x++) {
switch(field[y][x]) {
case CELL_TREE_YOUNG:
pixels.setPixelColor(ledMapping[i], pixels.Color(0, 1, 0));
break;
case CELL_TREE_AGED:
pixels.setPixelColor(ledMapping[i], pixels.Color(0, 10, 0));
break;
case CELL_TREE_DRY:
pixels.setPixelColor(ledMapping[i], pixels.Color(3, 2, 0));
break;
case CELL_FIRE:
pixels.setPixelColor(ledMapping[i], pixels.Color(25, 2, 0));
break;
case CELL_GLOWING:
pixels.setPixelColor(ledMapping[i], pixels.Color(1, 0, 0));
break;
default:
pixels.setPixelColor(ledMapping[i], pixels.Color(0, 0, 0));
break;
}
i++;
}
}
pixels.show();
}